2.2.5. Cycle Notation
Cycle notation is a method used to express permutations (transformations) in a concise and understandable way. This notation shows how elements are mapped to each other in the form of a cycle. Let’s illustrate this with an example.
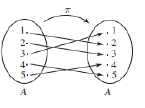
Here, notice that f(1) = 2, f(2) = 3, and f(3) = 1. As we can see, 1 goes to 2, 2 goes to 3, and 3 goes to 1, forming a cycle.
We write this as (123). f(4) = 5 and f(5) = 4, so there is also a cycle here. We write this as (45).
The cycle notation for the expression above is:
(123)(45)
2.2.6. Composition of Functions Definition
Let’s consider two functions, which we will define as f and g.
These two functions are defined as follows:
- f : A → B and g : B → C.
If we take an element x ∈ A, the function f(x) will give us a value, and this value is from the set B.
- Then, by applying the function g, we transform f(x) into g(f(x)). That is, we first find the value using the function f, and then process this value using the function g.
This operation can be written as g(f(x)) or simply (g ∘ f)(x). The function (g ∘ f) is called a composite function or composition. In other words:
- The function (g ∘ f) maps from set A to set C.
- The transformation described is (g ∘ f)(x) = g(f(x)).
The composition of functions follows the associative law, meaning that if:
f : A → B,
g : B → C,
then the following equality holds: h ∘ (g ∘ f) = (h ∘ g) ∘ f where h : C → D.
Thus, as long as the order of the functions h, g, and f is preserved, it does not matter which composite function is evaluated first.
2.2.7. Inverse Function Definition
The inverse of a function is a function that operates in the opposite direction of the original function. That is, it performs the reverse transformation of what the original function provides. This function is typically denoted as f⁻¹ and is read as “the inverse of f.” The fundamental property of the inverse function is that when the original function is applied to an input value, the output value can be recovered by applying the inverse function.
Mathematically, the inverse function can be defined as follows:
- f⁻¹(f(x)) = x
- (f⁻¹ ◦ f)(x) = x
For a function to have an inverse, the function must be bijective. This is because only bijective functions assign exactly one input value to each output value, meaning they are both injective (one-to-one) and surjective (onto). If a function is not bijective, it is not possible to find the inverse of every output value, as multiple input values may correspond to the same output, which prevents the definition of an inverse function.