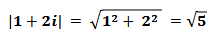The magnitude or norm of a vector is commonly expressed as the “length” of the vector and for a vector consisting of real or complex numbers, it is written as follows:

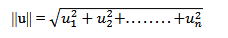
This calculation involves taking the square of each component of the vector, summing them, and then taking the square root. This process gives the magnitude or norm of the vector. An important note is that if a vector consists of complex numbers, the modulus (absolute value) of each component should be taken. This ensures that the norm is a real number.

If ||𝑢|| = 1, this vector is called a unit vector. A unit vector is a vector with a length of 1 and is usually represented with a hat symbol, for example, î. So far, two- and three-dimensional vectors have been defined relative to the origin. However, free vectors, meaning vectors that do not have a specific starting point, can be placed at any position as long as their length and direction are preserved.

As an example related to the topic, let’s define a vector consisting of a complex number and calculate its norm. Let’s consider the vector 1 + 2i and calculate its magnitude: