Before we dive into the topic, let’s first discuss what the Standard Orthonormal Basis is. This term is one of the simplest and most fundamental representations of a vector space in mathematics and linear algebra. Before defining this concept, we need to explain some basic terms. These terms are as follows:
(1) Basis, (2) Orthonormal

a. Basis

A basis is a set of vectors that can be used to construct all the vectors in a vector space. The basis vectors have the following properties:

• Linearly independent: None of the vectors in the basis is a combination of the others.
• Building blocks: They serve as building blocks to create any vector in the space.

b. Orthonormal

A basis is called orthonormal if it satisfies the following two properties:

• Orthogonality (perpendicularity): Each vector in the basis is perpendicular to the others, meaning the angle between them is 90 degrees.
• Normalization: The length (norm) of each vector in the basis is 1.

Now we can talk about the Standard Orthonormal Basis. This is the most basic and commonly used orthonormal basis. It is based on the standard coordinate system in Euclidean space.

• Two-dimensional space (ℝ²): The unit vectors along the x and y axes are the basis vectors. For example, 𝒆₁ = (1, 0) and 𝒆₂ = (0, 1).
• Three-dimensional space (ℝ³): The unit vectors along the x, y, and z axes are the basis vectors. For example, 𝒆₁ = (1, 0, 0), 𝒆₂ = (0, 1, 0), 𝒆₃ = (0, 0, 1).

4.2.2.1. Properties of Standard Orthonormal Bases:

• These vectors are perpendicular to each other and have a length of 1, thus forming an orthonormal basis.
• Any vector can be expressed as a linear combination of these basis vectors.

For example, the vector v = (x, y) in ℝ² can be expressed as:
v = x⋅𝒆₁ + y⋅𝒆₂

Now, the vectors defined in the Standard Orthonormal Basis are denoted as i and j, and they are written as follows:

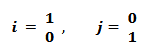
These vectors are unit vectors along the x and y axes, and they are perpendicular (orthogonal) to each other. They can be used to form any other vector in ℝ². These vectors are called the standard orthonormal basis of ℝ².

When we move to the third dimension, the standard orthonormal basis vectors in ℝ³ are as follows:

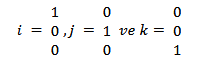
These vectors are the fundamental orthonormal vectors in ℝ³, and each is used as a unit vector along the x, y, and z axes. These vectors can be used to construct any vector in ℝ³.