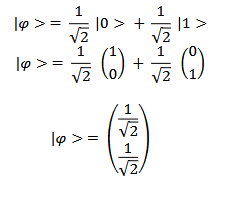A qubit, or quantum bit, is a concept that mathematically represents the state of the simplest quantum system. Qubits can exist in one of two distinct states, which are denoted as |0⟩ and |1⟩. A qubit can combine these two states to create a different state. In other words, a qubit can be written as a linear combination of the |0⟩ and |1⟩ vectors.

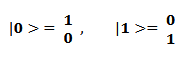
In a more general case, the state of the qubit can be expressed as

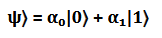
Here, α₀ and α₁ are complex numbers that represent the combination of the |0⟩ and |1⟩ states. This linear combination allows the qubit to exist in a different state. In other words, the qubit is a mixture of |0⟩ and |1⟩.

The values of α₀ and α₁ are complex numbers such that
|α₀|² + |α₁|² = 1. This constraint ensures that the total probability of the qubit is equal to 1. Therefore, the probability of the qubit being in the |0⟩ state is |α₀|², and the probability of it being in the |1⟩ state is |α₁|². The sum of these two probabilities is always equal to 1. The combination of states that a qubit has allows it to transition into different superposition states with varying probabilities.

Now, let’s immediately explain this with a superposition state: