5.2.1. Identity Matrix and Diagonal Matrices

An Identity Matrix is ​​a square matrix in which all elements on the main diagonal are 1 and all remaining elements are 0. For example;

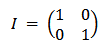
This is a special case for diagonal matrices, which are an important property of matrices. A diagonal matrix is a square matrix that has non-zero elements only on the main diagonal.

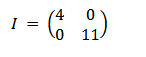
Identity matrices, when used with linear algebraic operations, serve a special function that does not alter vectors. Diagonal matrices are commonly used to model the specific properties of a system.

5.2.2. Transpose of a Matrix
The transpose of a matrix is a matrix obtained by swapping the rows and columns. In other words, the elements in the i-th row of the original matrix will be placed in the i-th column of the transposed matrix.
If A = 𝑎ᵢⱼ is a matrix, its transpose is expressed as 𝐴ᵀ = 𝑎ⱼᵢ. This is a mathematical operation that transforms each row and column into each other. Let’s provide an example related to this below:

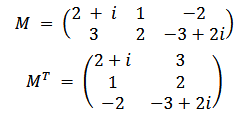
Transpose of matrices, especially in quantum computing with various transformations and often used in simulations.

5.2.3. Symmetric Matrices
A symmetric matrix is a matrix that is equal to its own transpose. That is, A = 𝐴ᵀ. If A = 𝑎ᵢⱼ, for the matrix to be symmetric, 𝑎ᵢⱼ = 𝑎ⱼᵢ must hold. In other words, it reflects the symmetry on the main diagonal of the matrix. For example:

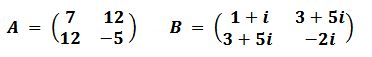
Both matrices are symmetric because A = Aᵀ and B = Bᵀ. These types of matrices are particularly important in quantum computing because symmetric matrices typically correspond to real eigenvalues that arise in measurement processes.

5.2.4. Conjugate Transpose (Hermitian Transpose)
The conjugate transpose of a matrix A is denoted as A⁺. The conjugate transpose is obtained by taking the transpose of A and then taking the complex conjugate of each element.

A⁺ = (A⁺)*

Here:

• The symbol T denotes the transpose, meaning it represents the swapping of rows and columns.
• The symbol ∗ represents the complex conjugate. In this operation, a complex number a + bi is transformed into
  a – bi.

Let’s work on an example related to this. First, we define a matrix A, then take its transpose, and finally take its complex conjugate.

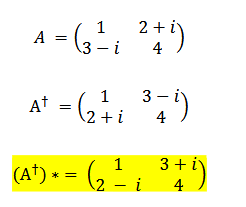
As can be understood from this, the expression (A⁺) is the Hermitian transpose. Now, we need to check if our matrix is Hermitian. For a matrix to be Hermitian (self-adjoint), it must satisfy A = A⁺. Looking at this example, we see that such an equality does not hold. Therefore, we can say that our matrix is not a Hermitian matrix.