5.2.5. Self-Adjoint or Hermitian Matrices
We have already touched on this topic in the example above, but here we will discuss it in more detail. In the field of quantum computing, self-adjoint or Hermitian matrices play an important role. The key property of these matrices is that their transpose is equal to their complex conjugate.
For a square matrix H to be self-adjoint, it means: The matrix H is equal to the complex conjugate of its transpose.
Mathematically, this property is expressed as:
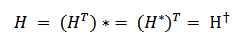
Where:
- H is the square matrix being examined,
- Hᵀ is the transpose of H,
- H* is the complex conjugate of H,
- 𝐻ᵀ is the Hermitian transpose of H.
An important property of self-adjoint matrices is that these matrices have real eigenvalues. This means that the values measured in quantum mechanics must be real numbers. Therefore, self-adjoint matrices are used in quantum computing to represent observables, which are the mathematical representations of measurable quantities.
Let’s work on an example related to this. First, we define a matrix H, then take its complex conjugate, followed by its transpose, and finally, we will check whether this matrix is self-adjoint, i.e., Hermitian.
Let Matrix H be as follows;
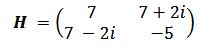
Let’s take the complex equivalent of the defined Matrix H.
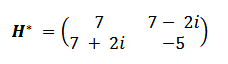
Let’s take the transpose of the expression whose Complex Equivalent we have taken.
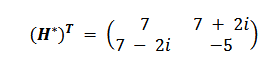
Looking at the matrix H, we see that it is equal to (H*)ᵀ, which proves that H is a Hermitian matrix, i.e., a self-adjoint matrix.
5.2.6. Normal Matrices
For a matrix to be normal, the transpose of the matrix multiplied by the matrix must be equal to the matrix multiplied by the transpose of the matrix. In other words, a matrix A is called a normal matrix if it satisfies the following mathematical condition:
𝐴 x 𝐴ᵀ = 𝐴ᵀ x 𝐴*
In this case, A is a normal matrix. Here, 𝐴ᵀ represents the transpose of the matrix A, meaning the rows and columns are swapped.
Let’s define a matrix A below and check whether it is a normal matrix.
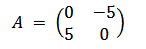
To check whether this matrix is normal, we will take the transpose of each matrix and multiply it by itself.
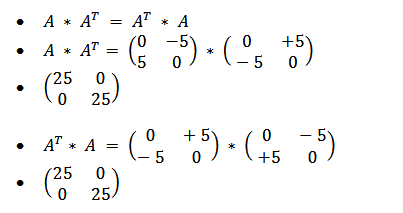
Since the condition 𝐴 x 𝐴ᵀ = 𝐴ᵀ x 𝐴 is satisfied, the matrix A is a normal matrix.
Let’s assume that we have two vectors, named A and B. Suppose that A is a row vector and B is a column vector. In this case, when we multiply the row vector by the column vector, it gives us a scalar, i.e., a number as the result.