In the context of quantum computing, we previously discussed row and column vectors. What we covered can be generalized to larger mathematical structures, particularly involving the use of matrices. If we increase the number of rows and columns of a matrix, we obtain larger-dimensional arrays. Such arrays are called matrices. Matrices not only track the evolution of quantum systems but also model the processes of quantum systems.

Let’s further develop the definition of a matrix. A matrix is a rectangular array consisting of m rows and n columns. The elements of this array can be real or complex numbers. The elements of a matrix are the numbers located in each cell of the matrix. These elements are typically defined by the row and column they are in within the matrix.

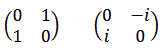
The two examples above are 2×2 matrices. The number of rows in a matrix forms the row vectors, while the number of columns forms the column vectors. Matrices are generally represented by uppercase letters.

In addition to the above notation, a more general form of a matrix, represented by A, can have each of its elements written according to its row and column numbers.

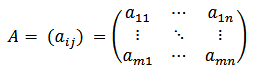
Here, 𝑎ᵢⱼ represents the element in the i-th row and j-th column of the matrix A. The type and properties of the matrix depend on the characteristics of the number of rows and columns, as well as the arrangement of these elements.