6.4.2. Quantum Algorithm’s Working Principle

At the beginning of the system, two qubits are initialized classically. The initial state is:

|0> |1>

• The first qubit is classically in the state 0. This state is also known as the ground state in quantum computers.
• The second qubit is classically in the state 1. This state is also known as the excited state in quantum computers.

For the quantum algorithm to work, these classical states need to be transformed into a quantum superposition. This transformation is done using the Hadamard Gate.

The Hadamard gate transforms a qubit from a classical state (e.g., ( |0> ) or ( |1>)) into a superposition state. Mathematically, the Hadamard gate performs the following transformation:

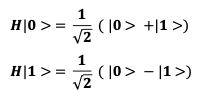
This transformation indicates that the qubit is in a combination of two different states at the same time:

• ∣0⟩ + ∣1⟩ meaning the system is in both ∣0⟩ and ∣1⟩ states.
• The second expression, ∣0⟩−∣1⟩ is the version of the same superposition with reversed signs (which is important for interference effects).

Now, when we apply the Hadamard Gate to both qubits simultaneously (H⊗H ), the system becomes:

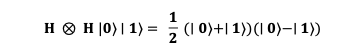
This expression now shows that both qubits are in an entangled superposition.

• The first qubit, ∣0⟩+∣1⟩ , is in a superposition state where both possibilities are represented with equal weight.
• The second qubit, ∣0⟩−∣1⟩ , is in a superposition that can create interference effects.

This situation creates the quantum mechanical property required for the algorithm to function, i.e., the creation of superposition.

6.4.3. The Function Operator U_f: Representation of Quantization

The function operator U_f is a quantum gate that adapts a classical function to quantum mechanics. Mathematically, U_f is defined as follows:

U_f ⎜x⟩ ⎜y⟩ = ⎜x⟩ ⎜y ⊕ f(x)⟩

Here:

• x: Represents the input to the function as the first qubit.
• y: Stores the output of the function as the second qubit.
• ⊕: Denotes the binary XOR operation, which is equivalent to modulo 2 addition.