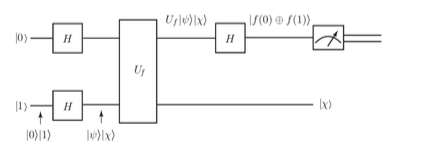
6.4.5.Deutsch Algorithm’s Quantum Circuit

The main components of this algorithm’s circuit are:

• Hadamard Gates: Used in the first and last steps to create superposition and interference.
• Function Operator ( U_f): Integrates the effect of the function into the quantum state.
• Measurement: The first qubit is measured to obtain the result.

The circuit operates as follows:

1. Hadamard gates are applied to the initial state |0> |1>
2. The ( U_f ) operator encodes f(0) and f(1) into the quantum state.
3. The final Hadamard gate is applied, followed by a measurement.

The quantum advantage in this algorithm is based on quantum mechanical principles such as superposition (being in multiple states simultaneously) and interference (states canceling or reinforcing each other):

• Superposition: The Hadamard gate processes |0> |1> simultaneously.
• Interference: The effect of ( U_f ) determines the measurement results based on whether the function is constant or balanced.

The Deutsch algorithm demonstrates that quantum computing can provide a fundamental speedup compared to classical computational methods. For more complex problems, the advantages of quantum algorithms become even more pronounced.