The Deutsch algorithm is one of the first algorithms that demonstrates the advantages of quantum computation over classical algorithms. The primary goal of this algorithm is to determine whether a function is constant or balanced with the minimum number of queries. In classical computation, at least two queries are required to obtain this information, while quantum computation can accomplish this with a single query. This represents an early indication of quantum superiority.

6.4.1. Problem Definition

Let us define a function: f : { 0, 1 } → { 0, 1 }
This function simply takes two-bit inputs and produces two-bit outputs. This function can be of one of the following two types:

a. Constant Function
As discussed earlier, constant functions produce the same output for both inputs (0 and 1). Mathematically: f(0) = f(1)
This implies that the function applies a fixed “rule” or “decision mechanism.”

For example:

If ( f(0) = 0 ) and ( f(1) = 0 ), the function always returns 0.

If ( f(0) = 1 ) and ( f(1) = 1 ), the function always returns 1.

Such functions generally represent a constant logic and produce an output independent of the input.

b. Balanced Function
Balanced functions produce different outputs depending on the input. Mathematically: f(0) ≠ f(1)
This means the function makes a decision based on the input and generates an equal number of outputs (one constant and one variable) in both cases.

For example:

If ( f(0) = 0 ) and ( f(1) = 1 ), the output is balanced between 0 and 1.

If ( f(0) = 1 ) and ( f(1) = 0 ), the output is balanced between 1 and 0.

These types of functions typically represent a conditional logic or “balancing” mechanism. In a classical algorithm, to determine this, both ( f(0) ) and ( f(1) ) must be queried. However, quantum computing can solve this problem with a single query by using superposition and interference. Let’s discuss this in more detail here.

1. Solution with Classical Algorithm

Classical algorithms examine the inputs sequentially to determine whether the function is constant or balanced. The outputs for both inputs (i.e., ( f(0) ) and ( f(1) )) must be checked.

For example:

• First, ( f(0) ) is computed. This operation gives the function’s output when the input is 0.
• Then, ( f(1) ) is computed. This operation gives the function’s output when the input is 1.
• By comparing the values of ( f(0) ) and ( f(1) ), it is determined whether the function is constant or balanced.

The drawback of this algorithm is that, in the worst case, two queries are required. For example, if ( f(0) = 0 ) and ( f(1) = 1 ), both ( f(0) ) and ( f(1) ) must be computed.

2. Solution with Quantum Algorithm

Quantum computing has the ability to solve this problem with a single query. This advantage relies on two fundamental properties of quantum mechanics: (1) Superposition and (2) Interference.

1. Superposition

In classical computing, the function can only be applied to one input at a time (e.g., ( f(0) ) or ( f(1) )). However, quantum computing can process inputs simultaneously in a superposition. Mathematically, the inputs can be expressed as:

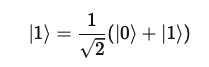
In this case, ( f(x) ), ( f(0) ), and ( f(1) ) are computed simultaneously. Thanks to superposition, the function is applied to both inputs at the same time.

2. Interference

Quantum algorithms use interference between the outputs from superposition states. Interference works by either canceling each other out (destructive interference) or reinforcing each other (constructive interference). In the Deutsch algorithm:

– The results of balanced functions cancel each other out. (Destructive Interference)

– The results of constant functions are strengthened.(Constructive Interference)