6.7.1. Definition of the Bernstein-Vazirani Problem
A function Bn → 𝐵 is given, where B = {0,1} , the set of binary values. This function is known to have the following form:
f(x) = x ∗ a
Here:
- x € Bn : An n-bit input.
- x € Bn: An unknown n-bit binary string (the value we want to find).
- x ∗ a : An operation called the mod 2 scalar product, calculated as:
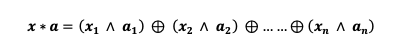
The goal of the Bernstein-Vazirani algorithm is to solve a problem more efficiently with quantum computing than a classical computer, which requires more queries. Specifically:
f(x) = x ∗ a
The algorithm’s objective is to determine this hidden string a
6.7.2 Classical Solution and Quantum Solution
Classical algorithms solve this problem by making n queries. As a result, the complexity of the classical algorithm is O(n). The quantum algorithm, using the properties of superposition and interference, finds a with only one query. Let’s now examine the steps of the algorithm in detail.
6.7.2.1 Initial State
Initially, n + 1 qubits are prepared as follows:
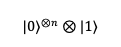
- The first n-qubits are in the |0⟩ state.
- The last qubit is in the |1⟩ state.
This represents the initial pure state of the quantum system.