6.12.4. Quantum Fourier Transform (QFT)

This topic will be explored in great detail in later sections, but for now, let us briefly discuss it. The Quantum Fourier Transform (QFT) is the quantum version of the classical Fourier transform and plays a fundamental role in the period-finding process. QFT reveals the frequency components of a function using quantum superposition. In Shor’s Algorithm, QFT is a part of the quantum circuit used to determine the period. Efficient implementation of QFT enhances the overall performance of the algorithm.

6.12.4.1. Definition and Properties of QFT

QFT takes an N-dimensional quantum state and applies the Fourier transform to it. Mathematically, a quantum state can be expressed as:

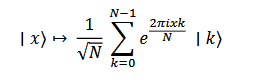
This transformation leverages the potential of quantum superposition, enabling parallel computation.

6.12.4.2. The Role of QFT in Shor’s Algorithm

In Shor’s Algorithm, the Quantum Fourier Transform (QFT) is used during the period-finding step to transform superpositioned data into the frequency domain. This enables the quantum computer to detect the period with high probability accurately.

6.12.5. Step-by-Step Examination of the Algorithm

To better understand the theoretical structure of Shor’s Algorithm, let us examine its steps in detail.

6.12.5.1. Input Preparation (Classical Stage)

• Problem Definition: A large integer N is provided, and the goal is to find its prime factors.
• Random Number Selection: A random integer a is selected in the range 2 ≤ a < N.
• Co-primality Check: If gcd(a, N) ≠ 1, then gcd(a, N) is a prime factor, and the algorithm terminates.

6.12.5.2. Period Finding (Quantum Stage)

• Function Definition: The function f(x) = a^x mod N is defined.
• Superposition Creation: The quantum computer creates a superposition of x values.
• QFT Application: QFT is applied to find the period of the function.
• Measurement: The quantum circuit is measured to obtain information about the period.

6.12.5.3. Analysis of Results and Determination of Prime Factors (Classical Stage)

• Using the Period: The period r obtained from the quantum stage is used to determine the prime factors.
• Prime Factor Calculation: If r is even and a^r/2 ≡ -1 mod N, then gcd(a^r/2 ± 1, N) is calculated to find the prime factors.