Complexity theory, which works on the efficiency of algorithms, examines how the running time or resource usage of an algorithm changes as the size of the inputs increases. The relative growth rates of functions are an important tool used to measure the time or space complexity of algorithms. Understanding these growth rates is essential for evaluating the effectiveness of algorithms, especially in large-scale problems or new computing paradigms like quantum computers.

2.4.1. Importance of Relative Growth

To evaluate the efficiency of an algorithm, it is necessary to determine how quickly the running time increases as the size of the inputs grows. The growth rates of different types of mathematical functions are crucial for understanding this process.

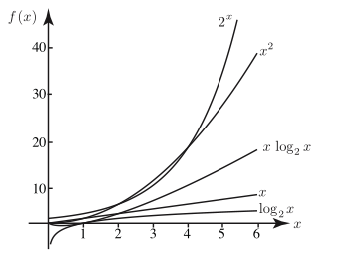
The above figure shows how the growth rates of functions change relative to each other as the input size (x) increases. In this context:

• Logarithmic functions grow very slowly and are commonly seen in efficient algorithms.
• Polynomial functions have a moderate growth rate; this growth is considered acceptable for many algorithms.
• Exponential functions grow very quickly and typically represent inefficient algorithms.

2.4.2. Types of Functions and Relative Growth

a. Logarithmic Functions : Logarithmic growth is one of the most efficient growth types for algorithms. For example, algorithms like binary search exhibit logarithmic growth. When the input size (n) doubles, the running time only increases by a constant amount.

• Mathematically, the logx growth rate is much slower compared to other types.
• Use Cases: Algorithms with logarithmic complexity are commonly preferred when working with large datasets.

b. Polynomial Functions : Polynomial growth is faster than logarithmic growth but grows slower than exponential growth.

• A polynomial with degree n = 2 is known as a quadratic function, x², and these algorithms typically exhibit moderate growth.
• Higher-degree polynomials (x³, x⁴) grow faster and generally require more resources.
• Use Cases: Algorithms with polynomial complexity offer acceptable performance in many practical problems. For example, some sorting algorithms have quadratic (O(n²)) time complexity.

c. Exponential Functions (2ˣ, 3ˣ) : Exponential growth is the most problematic growth type in terms of algorithm efficiency.

• As x increases, exponential functions grow extremely quickly. Therefore, algorithms with exponential growth generally become impractical in real-world use.
• For example, brute force algorithms (such as one that tries all possible paths on a graph) may exhibit exponential growth.
• Use Cases: Exponential complexity usually arises for problems that are difficult to solve. These types of algorithms may be used for smaller datasets or under limited circumstances.

2.4.3. Relative Growth and Algorithm Efficiency
The growth rates of functions are a fundamental criterion when evaluating how effective algorithms are for different problems:

1. Logarithmic Growth: Preferred when working with very large datasets; it is the most efficient growth type.
2. Polynomial Growth: Still an acceptable growth rate for large datasets.
3. Exponential Growth: A growth type that limits the realistic use of algorithms.

In the context of quantum computers, these growth rates become even more important. Quantum algorithms often offer significant advantages by reducing the exponential growth of classical algorithms to polynomial or lower complexity. Therefore, understanding the relative growth of functions is critical for grasping the relationship between quantum computing and complexity theory.