Earlier in this work, we defined the concept of a function as a relation that associates each element of one set with an element of another set. Here, we will extend this definition.
If the domain of the function consists of ordered pairs, then the domain is a Cartesian product. That is, for two sets A and B, the set 𝚨 × 𝚩 contains ordered pairs where each element a ∈ A and b ∈ B forms a pair.
A function defined on these ordered pairs is a function that returns a value for each (a, b) pair. This function is defined using three different sets:
Domain: Α × Β
Function: f: A × B → C
Co-Domain: C
2.6.1. f : B×B → B Defined Boolean Functions
When the domain of a function is B × B (i.e., the Cartesian product of two Boolean variables) and its co-domain is also the Boolean set B, this function becomes a Boolean function. The two fundamental concepts used here are logical operations such as “exclusive-or” (XOR) and “and.”
The Exclusive-OR (XOR) function outputs 1 when exactly one of the values x and y is 1. When both are 1, the output is 0. The truth table for this function is as follows:
| x | y | x ⊕ y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
This function is also known as an XOR gate or the classical CNOT function and is frequently used in digital circuits.
The AND function produces a result of 1 when both x and y are 1. Otherwise, the result is 0. The truth table for this function is as follows:
| x | y | x ∧ y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
These functions and similar ones operate with binary values and form the foundation of digital logic circuits.
2.6.2. Functional Completeness and Universality
This concept is fundamental in fields such as mathematical logic and digital circuit design. A set of operations is said to be functionally complete if it is sufficient to express every possible logical expression within that set. Functional completeness means that a set of logical operations has the capacity to generate all logical operations that can be expressed by any truth table. For example, the set {AND ∧, NOT ¬} is functionally complete because, by using these two operations, we can derive all other logical operations (OR, XOR, NAND, NOR, etc.).
Let’s now discuss how the other gates can be derived.
OR (∨) Operation
Logically, A ∨ B means that either A or B is true. This can be expressed using AND and NOT gates as follows:
A ∨ B = ¬(¬A ∧ ¬B)
XOR (⊕) Operation
XOR outputs true when A and B are different. This can be expressed using AND and NOT gates as follows:
A ⊕ B = (A ∧ ¬B) ∨ (¬A ∧ B)
NAND (NOT AND) Operation
A ↑ B = ¬(A ∧ B)
NOR (NOT OR) Operation
A ↓ B = ¬(A ∨ B)
2.6.3. Injectivity and Inversibility
The injectivity of a function is important. If a function is not injective, it means that the function is not invertible. Inversibility refers to a function being reversible. This means that when we know the output of a function, we can uniquely determine which input values correspond to it.
a. Injective Function: For each output, there is only one input combination. In other words, the function is invertible, and knowing the output allows us to unambiguously predict the input.
b. Non-Injective Function: There are multiple input combinations that produce the same output. For example, the combinations (0,1) and (1,0) both produce the same output (1) for the XOR operation. In this case, it is not possible to determine the inputs definitively by only looking at the output.
Non-injectivity is an important concept in digital circuits and especially in quantum computing. This is because invertibility ensures that inputs can be recovered from the outputs. If a function is not invertible, the input information is lost, and it is impossible to recover this information by using the output.
2.6.4. Inversibility in Digital Systems and Applications
Digital logic circuits typically use non-injective functions. For example, logic gates like XOR gates are examples of non-injective functions. However, some computations or operations may require invertibility.
In advanced computing areas such as quantum computing, invertibility becomes much more critical. Unlike classical computing, quantum computing relies on operations being reversible. That is, in a quantum algorithm, it is possible to reverse the result after an operation. This is part of the potential power of quantum computers.
For example, it is difficult to invert a classical XOR gate because it is not possible to determine the inputs just by looking at the output. However, in quantum logic gates, invertibility can be ensured, making such operations easier and enabling computations without information loss.
2.6.5. Boolean Functions Defined on 𝒇 = 𝑩² → 𝑩²
In this section, we will examine Cartesian products where both the domain and codomain are B×B = 𝐵². The expression B×B = 𝐵² means that the input and output are pairs of Boolean values. The set B is expressed as {0, 1}, and in this case, 𝐵² contains all possible binary pair combinations: {00, 01, 10, 11}.
We know that the classical CNOT gate is not invertible. Here, we will take one step further and discuss the Feynman CNOT gate. The Feynman CNOT gate is mathematically expressed as:
- 𝑭𝑫(x, y) = (x, x ⊕ y)
This defined function takes an input pair (x and y) and, while leaving the x value unchanged, modifies the y value by applying the XOR operation with x. The XOR operation results in 1 when the two values are different, and 0 when they are the same.
The Feynman CNOT gate is a bijective function, meaning it is both injective and surjective. This means it is an invertible gate. This gate is designed for classical computers and is used in classical Boolean operations. The gate is the classical analog of the quantum CNOT gate but does not carry any quantum mechanical properties.
The truth table for this gate is as follows :
| Input (x and y) | Output (x x ⊕y ) |
| 0,0 | 0,0 |
| 0,1 | 0,1 |
| 1,0 | 1,1 |
| 1,1 | 1,0 |
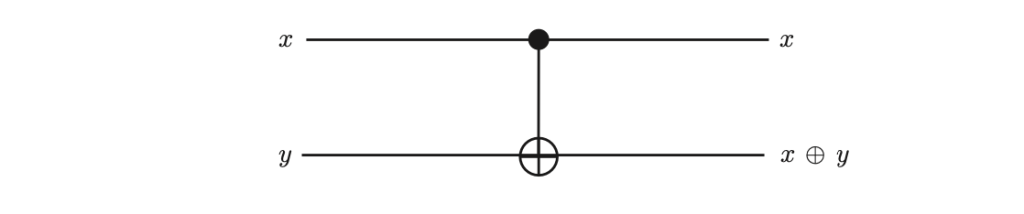
Feyman CNOT Gate Demonstration
2.6.6. Other Boolean Functions
2.6.6.1. Toffolo Gate veya CCNOT Gate
Let’s consider a 3-input 𝑻𝑫 function. We already know that if it has 3 inputs, mathematically, this function will be defined as 𝑩³ → 𝑩³.
This function is defined as:
𝑻𝑫(x, y, z) = (x, y, z ⊕ (x ∧ y))
This defined function is known as the Toffoli gate or CCNOT gate.
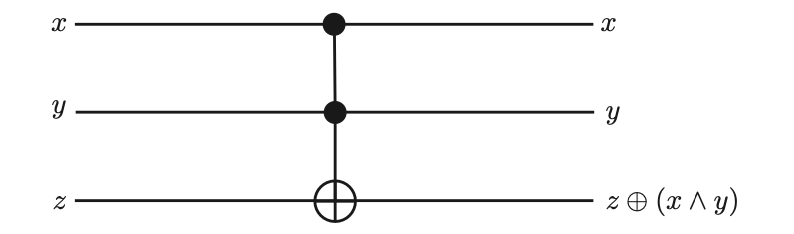
The function defined above is represented as shown above.
The operation of this gate involves taking three input values and performing certain operations on them to produce three output values. Here are the details of these operations:
- The first two inputs (x and y) are directly preserved in the output; that is, the first two elements of the output are the x and y values from the input.
- The third output element (the new value of z) is calculated by performing an XOR operation between the old value of z and the result of the AND operation between x and y.
The truth table for this gate is as follows:
| Input (x,y,z) | Output (x,y,z) |
| 0,0,0 | 0,0,0 |
| 0,0,1 | 0,0,1 |
| 0,1,0 | 0,1,0 |
| 0,1,1 | 0,1,1 |
| 1,0,0 | 1,0,0 |
| 1,0,1 | 1,0,1 |
| 1,1,0 | 1,1,1 |
| 1,1,1 | 1,1,0 |
When z is set to 0, the Toffoli gate computes the function x ∧ y. In this case,
z ⊕ (x ∧ y) simply returns the value of x ∧ y because XOR with 0 does not change the value of any operand.
- When x = y = 1, the operation z ⊕ 1 is applied, which produces the NOT operation on z because XOR with 1 inverts the value of the operand.
- When z is set to 1, the operation 1 ⊕ (x ∧ y) computes the NAND function, because XOR with 1 inverts the value of the operand.
- Specific inputs such as 𝑻𝑫(x, 1, 0), 𝑻𝑫(1, y, 0), and 𝑻𝑫(x, x, 0) ensure that the input values are directly copied to the output. This property facilitates the preservation and management of data during computations.
The Toffoli gate defines a universal set of functions required for performing reversible computations on digital computers. It is also an important operator in quantum computers, but on its own, it is not universal for quantum computing.
This gate is a critical tool for both classical computer science and quantum computer science, standing out for its ability to perform various logical operations in a reversible manner.
2.6.6.2. Digital Peres Gate
Let’s consider a 3-input 𝑷𝑫 function. We already know that if it has 3 inputs, mathematically, this function will be defined as 𝑩³ → 𝑩³.
𝑷𝑫(x, y, z) = (x, y ⊕ x, z ⊕ (x ∧ y))
This function is called the Digital Peres Gate or Half-Adder. This function is bijective. This gate is formed by the combination of the CNOT gate and the Toffoli gate. This structure plays a significant role in quantum computing and provides deep insights into the functionality of the relevant gates.
| Girdi (x, y, z) | Çıktı (x, y⊕x, z⊕(x∧y)) |
| 0, 0, 0 | 0, 0, 0 |
| 0, 0, 1 | 0, 0, 1 |
| 0, 1, 0 | 0, 1, 0 |
| 0, 1, 1 | 0, 1, 1 |
| 1, 0, 0 | 1, 1, 0 |
| 1, 0, 1 | 1, 1, 1 |
| 1, 1, 0 | 1, 0, 1 |
| 1, 1, 1 | 1, 0, 0 |
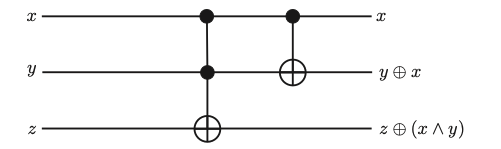
The function defined above is shown as in the figure above.