6.7.1. Definition of the Bernstein-Vazirani Problem

A function Bⁿ → 𝐵 is given, where B = {0,1} , the set of binary values. This function is known to have the following form:

f(x) = x ∗  a

Here:

• x € Bⁿ : An n-bit input.
• x € Bⁿ: An unknown n-bit binary string (the value we want to find).
• x ∗  a : An operation called the mod 2 scalar product, calculated as:

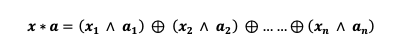
The goal of the Bernstein-Vazirani algorithm is to solve a problem more efficiently with quantum computing than a classical computer, which requires more queries. Specifically:

f(x) = x ∗  a

The algorithm’s objective is to determine this hidden string a

6.7.2 Classical Solution and Quantum Solution

Classical algorithms solve this problem by making n queries. As a result, the complexity of the classical algorithm is O(n). The quantum algorithm, using the properties of superposition and interference, finds a with only one query. Let’s now examine the steps of the algorithm in detail.

6.7.2.1 Initial State

Initially, n + 1 qubits are prepared as follows:

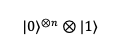
• The first n-qubits are in the |0⟩ state.
• The last qubit is in the |1⟩ state.

This represents the initial pure state of the quantum system.