6.7.2.2. Creating the Superposition State

Initially, Hadamard Gates are applied to the start state, putting the qubit into superposition:

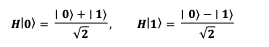
All n+1 qubits are subjected to the Hadamard Gate, achieving this superposition state:

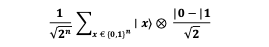
This expression represents all possible n-bit x values simultaneously.

6.7.2.3. Applying the Oracle

The Oracle is a quantum circuit that implements the function f(x). The Oracle’s task is to apply a phase shift:

|x> ⊕ |y> → |x> ⊕ |y> ⊕ f(x)>

After this operation, the last qubit contains f(x). However, if the last qubit is in the state (|0> – |1>) / √2, the phase shift is reflected in the system as follows:

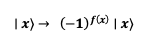
Therefore, the new state of the system becomes:

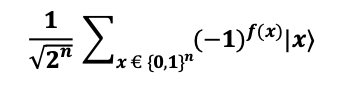
6.7.2.4. Reapplying Hadamard Gates

Now, Hadamard gates are reapplied to all n-qubits. This process transforms phase shifts into meaningful information through interference:

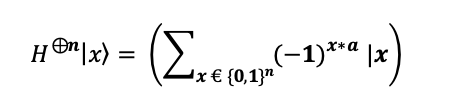
The mathematical result of the Hadamard transformation is:

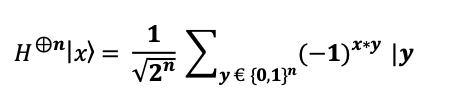
This transformation results in the system being in the state:

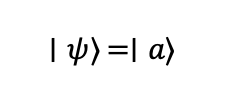
As a result, the quantum state solely represents |a>.